오늘 배운 내용
오늘은 과대적합, 과소적합의 의미와 그 해결법을 공부했다.
해결법의 종류는 여러가지가 있지만, 그 중 배치 정규화, 가중치 초기화, 정칙화를 중심으로 공부했다.
이번 포스팅에서는 배치 정규화, 가중치 초기화를 다룰 것이다.
과대적합, 과소적합의 의미
과대적합(Overfitting)
- 모델이 훈련 데이터에서는 우수하게 예측하지만, 테스트 데이터에서는 제대로 예측하지 못해 오차가 크게 발생하는 것
과소적합(Underfitting)
- 훈련 데이터와 테스트 데이터 모두에서 낮은 성능을 보이는 것
모델 선택 실패
과대적합과 과소적합은 모델을 변경해 문제를 완화할 수 있다.
과대적합의 경우 모델의 구조가 너무 복잡해 훈련 데이터에만 의존하게 되어 성능이 저하된다.
반대로 과소적합의 경우 모델의 구조가 너무 단순해 데이터의 특징을 제대로 학습하지 못 한 경우이다.
그러므로 모델을 변경하거나 모델 구조를 개선해야 한다.
편향-분산 트레이드오프
모델이 훈련 데이터와 새로운 데이터에 대해서도 우수한 성능을 보이려면 낮은 평향과 낮은 분산을 가져야 한다.
분산이 높으면 추정치에 대한 변동 폭이 커지며, 데이터가 갖고 있는 노이즈까지 학습 과정에 포함돼 과대적합 문제를 발생시킨다.
편향이 높으면 추정치가 항상 일정한 값을 갖게 될 확률이 높아져 데이터의 특징을 제대로 학습하지 못 해 과소적합 문제를 발생시킨다.
이때, 편향과 분산은 서로 반비례하기 때문에 적당히 분산과 편향의 균형을 맞춰 최적의 모델 복잡도를 찾아야 한다.
과대적합, 과소적합 문제 해결 방법
1. 데이터 수집
- 모델이 더 일반적인 규칙을 찾을 수 있게 학습 데이터의 수를 늘린다.
2. 피처 엔지니어링
- 만약 새로운 데이터의 수집이 어려운 상황에서는 기존 데이터에서 변수나 특징을 추출하거나 피처를 더 작은 차원으로 축소한다. 따라서 모델이 학습하기 쉬운 데이터의 형태로 변환하면 노이즈에 더 강건한 모델을 구축할 수 있다.
3. 모델 변경
- 과대적합은 데이터에 비해 강력한 모델을 사용할 때 발생하고, 과소적합은 데이터에 비해 간단한 모델을 사용할 때 발생한다.
4. 조기 중단
- 모델 학습 시 검증 데이터세트(validation_dataset)로 성능을 지속적으로 평가해 모델의 성능이 저하되기 전에 학습을 멈춘다.
5. 배치 정규화
- 모델의 계층마다 평균과 분산을 조정해 내부 공변량 변화를 줄인다.
6. 가중치 초기화
- 모델의 매개변수를 최적화하기 전에 가중치 초기값을 설정하여 학습 시 기울기가 매우 작아지거나 커지는 문제를 방지한다.
7. 정칙화
- 목적 함수에 페널티를 부과해서 과적합을 방지한다.
배치 정규화, 가중치 초기화는 아래에서 더 자세히 다루겠다.
1. 배치 정규화(Batch Normalization)
일반적으로 인공신경망을 학습할 때 입력값을 배치 단위로 나눠 학습을 진행한다.
배치 단위로 나눠 학습하는 경우 상위 계층의 매개변수가 갱신될 때마다 현재 계층에 전달되는 데이터의 분포도 변경되는데, 각 계층은 배치 단위의 데이터로 인해 계속 변화하는 입력 분포를 학습해야 하기 때문에 성능과 안정성이 낮아져 학습 속도가 느려진다.
이를 내부 공변량 변화라고 하는데, 배치 정규화는 이것을 줄여 과적합을 방지하는 기술이다.
배치 정규화는 미니 배치의 입력을 정규화하는데,
예를 들면 입력값이 [100, 1, 1], [0, 0.01, 0.01] 이라면 두 배열의 값 모두 [1.4142, -0.7071, -0.7071]로 정규화한다.
import torch
from torch import nn
# 텐서 초기값
x = torch.FloatTensor(
[
[-0.6577, -0.5797, 0.6360],
[0.7392, 0.2145, 1.523],
[0.2432, 0.5662, 0.322]
]
)
print(nn.BatchNorm1d(3)(x))# 결과
tensor([[-1.3246, -1.3492, -0.3756],
[ 1.0912, 0.3077, 1.3685],
[ 0.2334, 1.0415, -0.9930]], grad_fn=<NativeBatchNormBackward0>)
예시 텐서는 1차원이므로 nn.BatchNorm1d 함수를 사용했다.
그 이상의 차원에 대해서는 아래의 함수를 사용한다.
# 1,2,3D
nn.BatchNorm1d(num_features)
# 4D
nn.BatchNorm2d(num_features)
# 5D
nn.BatchNorm3d(num_features)
장점
- 내부 공변량 변화를 줄이기 때문에 층별 입력 분포가 일정하게 유지된다. 따라서 안정적인 학습 가능
- 더 큰 learning rate를 써도 안정적이게 되는데, 이로 인해 수렴 속도가 빨라져서 학습 속도 또한 빨라진다.
- 과적합 완화 가능
단점
- 너무 작은 배치를 쓰면 통계량 추정이 불안정해져 배치 정규화의 성능이 떨어진다. (작은 배치에서는 LayerNorm 또는 GroupNorm을 사용한다.)
- RNN과 같은 순환 구조에서는 적용이 어렵다
- 각 미니배치마다 평균/분산 계산이 필요해서 연산량이 증가한다.
2. 가중치 초기화(Weight Initialization)
가중치 초기화란 모델의 초기 가중치 값을 설정하는 것을 말한다.
적절한 초기값을 설정한다면 기울기 폭주(Gradient Exploding)나 기울기 소실(Gradient Vanishing) 문제를 해결할 수 있으며, 모델의 수렴 속도를 향상시킬 수 있다.
이제 가중치 초기화의 방법에 대해 알아보자.
1. 상수 초기화
초기 가중치 값을 모두 같은 값으로 초기화하는 것을 말한다.
대표적으로 0, 1, 특정 값, 단위행렬, 디랙 델타 함수(Dirac Delta Function) 값 등이 있다.
하지만 이 방법은 일반적으로 사용되지 않는다. 모든 가중치 초기값을 같은 값으로 초기화하면 배열 구조의 가중치에서는 문제가 발생한다. 이러한 문제는 대칭 파괴(Breakin Symmetry) 현상으로 인해 모델 학습을 불가능하게 만든다.
# tensor을 val로 초기화
torch.nn.init.constant_(tensor, val)
# tensor을 1로 초기화
torch.nn.init.ones(tensor)
# tensor을 0으로 초기화
torch.nn.init.zeros(tensor)
# 대각선을 1로 채우고 다른 곳은 0으로 초기화 (단위행렬)
torch.nn.init.eye_(tensor)
# 디랙 델타 함수로 초기화 (3, 4, 5차원 텐서만 가능)
torch.nn.init.dirac_(tensor)
# 균등 분포 U(a,b)로 초기화
torch.nn.init.uniform_(tensor, a, b)2. 무작위 초기화
가중치의 값을 무작위 값이나 특정 분포 형태로 초기화하는 것을 말한다.
대표적으로 무작위(random), 균등 분포(Uniform Distribution), 정규 분포(Normal Distribution), 잘린 정규 분포(Truncated Normal Distribution), 희소 정규 분포 초기화(Sparse Normal Distribution Initialization) 등이 있다.
계층이 적거나 하나만 있는 경우에는 보편적으로 사용할 수 있지만, 계층이 많아지고 깊어질수록 기울기 소실 문제가 발생할 수 있다는 단점이 있다.
# 정규 분포 초기화: N(mean, var)
torch.nn.init.normal_(tensor, mean, std)
# 잘린 정규 분포 초기화: N(mean, var)[a,b]
torch.nn.init.runc_normal_(tensor, mean, std, a, b)
# 희소 정규 분포 초기화: sparsity 비율만큼 N(0, 0.01)로 초기화
torch.nn.init.sparse_(tensor, sparsity)3. 제이비어 & 글로럿 초기화
제이비어 글로럿과 요슈아 벤지오가 2010년에 제안했으며, 균등 분포나 정규 분포를 사용해 가중치를 초기화하는 방법이다.
(1) 균등분포:
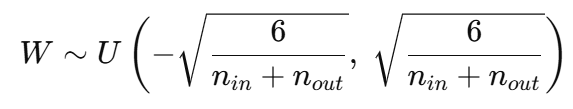
(2) 정규 분포:

용어 설명:

제이비어 초기화와 확률 분포 초기화의 주요한 차이점은 동일한 표준 편차를 사용하지 않고 은닉층의 노드 수에 따라 다른 표준편차를 할당한다는 점이다. 즉, 이전/다음 층의 노드 개수에 따라 표준편차가 계산된다.
제이비어 초기화는 입력 데이터의 분산이 출력 데이터에서 유지되도록 가중치를 조절하므로 Sigmoid나 Tanh를 활성화 함수로 사용하는 네트워크에서 효과적이다.
그 이유는?
- 입력 벡터와 가중치 벡터의 가중합(Wx)을 활성화 함수에 넣는 계산 과정에서, 만약 활성화 함수가 Sigmoid나 Tanh일 때,
- 가중치가 너무 크다면 ? Wx 값이 너무 커진다.
- 출력이 0 또는 1(Sigmoid), -1 또는 1(Tanh) 근처로 포화된다.
- 그렇게 되면 아래의 과정 때문에 기울기는 0에 가깝게 된다.
- Sigmoid
- 기울기 = σ′(z) = σ(z)(1−σ(z))
- σ(z) ≈ 1 → σ'(z) ≈ 1×(1-1) = 0
- σ(z) ≈ 0 → σ'(z) ≈ 0×(1-0) = 0
- Tanh
- 기울기 = tanh′(z) = 1 − tanh^2(z)
- tanh(z) ≈ 1 → tanh'(z) ≈ 0
- tanh(z) ≈ -1 → tanh'(z) ≈ 0
- Sigmoid
- 가중치가 너무 작다면? Wx 값이 너무 작아진다.
- 기울기 소실 문제 발생
- 따라서 출력이 적절한 범위에 있어야 학습이 잘 된다.
- 그러므로 입출력 뉴런 수를 고려해서 가중치를 초기화하는 제이비어 초기화를 사용하면
- 층을 지나도 출력이 적당한 범위를 유지한다. -> 입출력 분산이 유지되게 하는 목표 달성
# 균등 분포
torch.nn.init.xavier_uniform_(tensor, gain=1.0)
# 정규 분포
torch.nn.init.xavier_normal_(tensor, gain=1.0)4. 카이밍 & 허 초기화
카이밍 허가 2015년에 제안했으며, 제이비어 초기화와 마찬가지로 균등 분포나 정규 분포를 사용하는 방식이다.
ReLU 계열을 사용할 때 죽은 뉴런 문제를 줄이기 위해 가중치의 분산을 적절히 유지하는 방법이다.
(1) 균등 분포

(2) 정규 분포

위의 수식에서 확인할 수 있듯이 현재 계층의 뉴런 수를 기반으로만 가중치를 초기화한다.
ReLU 계열 함수를 활성화 함수로 사용하는 네트워크에서 효과적이다.
단점은 Sigmoid, Tanh처럼 출력 범위가 제한된 함수에는 적합하지 않다.
# 균등 분포
torch.nn.init.kaiming_uniform_(tensor, a=0)
# 정규 분포
torch.nn.init.kaiming_normal_(tensor, a=0)5. 직교 초기화
특이값 분해(Singular Value Decomposition, SVD)를 활용해 자기 자신을 제외한 나머지 모든 열, 행 벡터들과 직교이면서 동시에 단위 벡터인 행렬을 만드는 방법이다.
직교 행렬의 고유값의 절대값은 1이기 때문에 행렬 곱을 여러 번 수행하더라도 기울기 폭주나 기울기 소실이 발생하지 않는다.
따라서 RNN에서 기울기가 사라지는 문제를 방지하는 데 사용한다.
직교 초기화는 모델이 특정 초기화 값에 지나치게 민감해지므로 순방향 신경망에서는 사용하지 않는다.
torch.nn.init.orthogonal_(tensor, gain=1)
# gain은 배율 계수를 의미가중치 초기화 예시 코드:
AIFFEL_practice/pytorch/advanced/2_Weight_Initialization.ipynb at main · choiwonjini/AIFFEL_practice
Contribute to choiwonjini/AIFFEL_practice development by creating an account on GitHub.
github.com
정칙화(Regularization)는 정리할 내용이 다소 길어서 다음 포스팅에서 자세히 다루겠다.
https://choiwonjin.tistory.com/55
[10/14] 아이펠 리서치 15기 TIL | 과적합 해결법 (정칙화)
이전 포스팅:https://choiwonjin.tistory.com/54 [10/14] 아이펠 리서치 15기 TIL | 과적합 해결법 (배치 정규화 & 가중치 초기화)오늘 배운 내용오늘은 과대적합, 과소적합의 의미와 그 해결법을 공부했다.해
choiwonjin.tistory.com
느낀 점, 어려웠던 점
'AI > ML' 카테고리의 다른 글
| [10/15] 아이펠 리서치 15기 TIL | 텍스트 & 이미지 데이터의 증강 및 변환 (0) | 2025.10.15 |
|---|---|
| [10/14] 아이펠 리서치 15기 TIL | 과적합 해결법: 정칙화(Regularization) (0) | 2025.10.15 |
| [10/2] 아이펠 리서치 15기 TIL | Loss F, Activation F, Optimizer (0) | 2025.10.12 |
| [10/1] 아이펠 리서치 15기 TIL | ML 학습 방법론, ML 아키텍처, MLOps (0) | 2025.10.09 |
| [9/25] 아이펠 리서치 15기 TIL | Regularization(Lasso, Ridge) & Clustering(K-means, DBSCAN) (0) | 2025.09.25 |



