반응형
1. 오늘 배운 내용
오늘은 Regularization, Unsupervised learning 두 노드를 배웠다.
Regularization
1. Regularization과 Normalization
- Regularization(정칙화)
- 오버피팅(overfitting)을 해결하기 위한 방법 중의 하나
- L1, L2 Regularization, Dropout, Batch normalization 등이 있다.
- 모델에 제약 조건을 걸어서 모델의 train loss를 증가시키는 역할
- train loss는 약간 증가하지만 결과적으로, validation loss나 최종 test loss를 감소시키려는 목적
- Normalization(정규화)
- 트레이닝에 적합하게 전처리하는 과정
- z-score, minmax scale 등이 해당된다.
- 모든 피처(변수) 값의 범위(단위)를 동일하게 해서 데이터의 왜곡을 막을 수 있다.
2. L1, L2 Regularization [Lasso & Ridge]
L1 - Lasso: 손실 함수에 가중치의 절대값 합을 추가
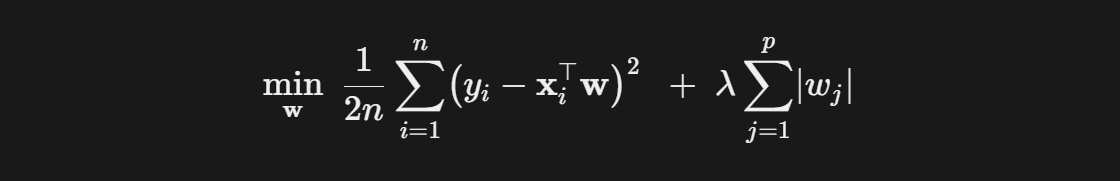
L2 - Ridge: 손실 함수에 가중치의 제곱 합을 추가

공통점
- 회귀계수(가중치)에 패널티를 부과하여 과적합을 방지한다.
- 하이퍼파라미터 λ를 통해 규제 강도를 조절한다.
차이점
| 구분 | L1 정칙화 (Lasso) | L2 정칙화 (Ridge) |
| 가중치 효과 | 일부 가중치를 정확히 0으로 만들어 변수 선택 효과(희소성) | 가중치를 0으로 만들진 않고 작게만 줄임 |
| 모델 특성 | 변수 선택에 유리, 해석 쉬움 | 모든 변수 사용, 안정적 추정 |
| 수학적 특성 | 비분화 지점 존재 → 최적화가 더 복잡할 수 있음 | 미분 가능 → 해 분석이 더 단순함 |
| 사용 추천 상황 | 변수 중 일부만 중요할 때 (feature selection 필요) | 대부분 변수가 중요하지만 과적합 방지가 필요할 때 |
| 이상치 | 강건함 | 약함 (제곱의 영향) |
정리하면,
- L1(Lasso)는 가중치가 적은 벡터에 해당하는 회귀계수를 0으로 보내면서 차원 축소와 비슷한 역할을 하고,
- L2(Ridge)는 계수를 0으로 보내지는 않지만 제곱 텀이 있기 때문에 Lasso 보다는 수렴 속도가 빠르다는 장점이 있다.
예를 들면,
- A=[1,1,1,1,1], B=[5,0,0,0,0]의 경우 L1-norm은 같지만, L2-norm은 같지 않다.
- 즉, Ridge에서는 제곱 텀에서 결과에 큰 영향을 미치는 값은 더 크게, 결과에 영향이 적은 값들은 더 작게 보내면서 수렴 속도가 빨라지는 것.
3. Dropout
- 드롭아웃 기법이 나오기 전의 신경망은 fully connected architecture로 모든 뉴런들이 연결되어 있었다.
- 확률적으로 랜덤하게 몇 가지의 뉴런만 선택하여 정보를 전달하는 과정
- fully connected layer에서 오버피팅이 생기는 경우에 dropout layer를 추가하는 방식
Dropout의 확률 조정
- 확률을 너무 높이면 (비활성화된 뉴런의 비중을 높이면) 모델 안에서 값들이 제대로 전달되지 않으므로 학습이 잘 되지 않고,
- 확률을 너무 낮추는 경우에는 fully connected layer와 같이 동작한다.
군집화(Clustering)
명확한 분류 기준이 없는 상황에서도 데이터들을 분석하여 가까운(또는 유사한) 것들끼리 묶어 주는 작업
1. K-means Clustering
주어진 데이터들을 k 개의 클러스터로 묶는 알고리즘
K-mean 알고리즘의 순서
- 원하는 클러스터의 수(K)를 결정한다.
- 클러스터의 수와 같은 K개의 중심점(centroid)을 무작위로 생성한다.
- 중심점이 바뀌지 않을 때까지 아래의 (1, 2)를 반복 시행한다.
- 중심점을 바탕으로 모든 점들과 새로 조정된 중심점 간의 유클리드 거리를 계산한 후, 가장 가까운 거리를 가지는 클러스터에 해당 점을 할당한다.
- 특정 클러스터에 속하는 모든 점들의 평균값으로 중심점을 재조정한다.
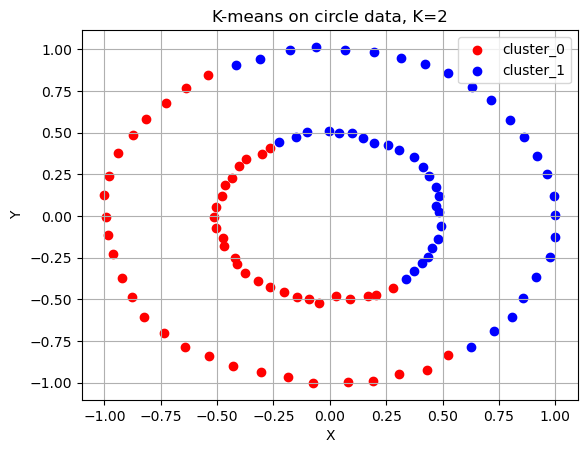
아래 그림은 K=2일 경우.

하지만,
- 군집의 개수(K 값)를 미리 지정해야 하기 때문에 이를 알거나 예측하기 어려운 경우에는 사용하기 어렵다.
- 유클리드 거리가 가까운 데이터끼리 군집이 형성되기 때문에 데이터의 분포에 따라 유클리드 거리가 멀면서 밀접하게 연관되어 있는 데이터들의 군집화를 성공적으로 수행하지 못할 수 있다.
예시로, 다음의 경우에는 k-means가 잘 동작하지 않는다.
(1) 원형 분포
(2) 달 모양 분포

2. DBSCAN
- Density-Based Spatial Clustering of Applications with Noise의 약자
- 이름 그대로 밀도 기반의 클러스터링 방법이다.
용어 정리
- epsilon: 클러스터의 반경
- minPts: 클러스터를 이루는 개체의 최솟값(사용자 지정)
- neighborhood(이웃): epsilon 거리 내에 있으면 이웃이라고 한다.
- core point: 반경 epsilon 내에 minPts 개 이상의 점이 존재하는 점
- border point: 반경 epsilon 내에 minPts 개 이하의 점이 존재하고, core point의 이웃인 점
- noise point: 군집에 포함되지 못하는 점 (core, border이 아니면 모두 noise)

DBSCAN 알고리즘의 순서
- 임의의 점 p를 선정한다.
- p를 포함하여 주어진 클러스터의 반경(elipson) 안에 포함되어 있는 점들의 개수를 센다.
- 만일 해당 원에 minPts 개 이상의 점이 포함되어 있으면, 해당 점 p를 core point로 간주하고 원에 포함된 점들을 하나의 클러스터로 묶는다.
- 해당 원에 minPts 개 미만의 점이 포함되어 있으면, 일단 pass.
- 모든 점에 대하여 돌아가면서 2-3 번의 과정을 반복하는데, 만일 새로운 점 p가 core point가 되고 이 점이 기존의 클러스터(p를 core point로 하는)에 속한다면, 두 개의 클러스터는 연결되어 있다고 하며 하나의 클러스터로 묶는다.
- 모든 점에 대하여 클러스터링 과정을 끝냈는데, 어떤 점을 중심으로 하더라도 클러스터에 속하지 못하는 점이 있으면 이를 noise point로 간주한다. 또한, 특정 군집에는 속하지만 core point가 아닌 점들을 border point라고 칭한다.
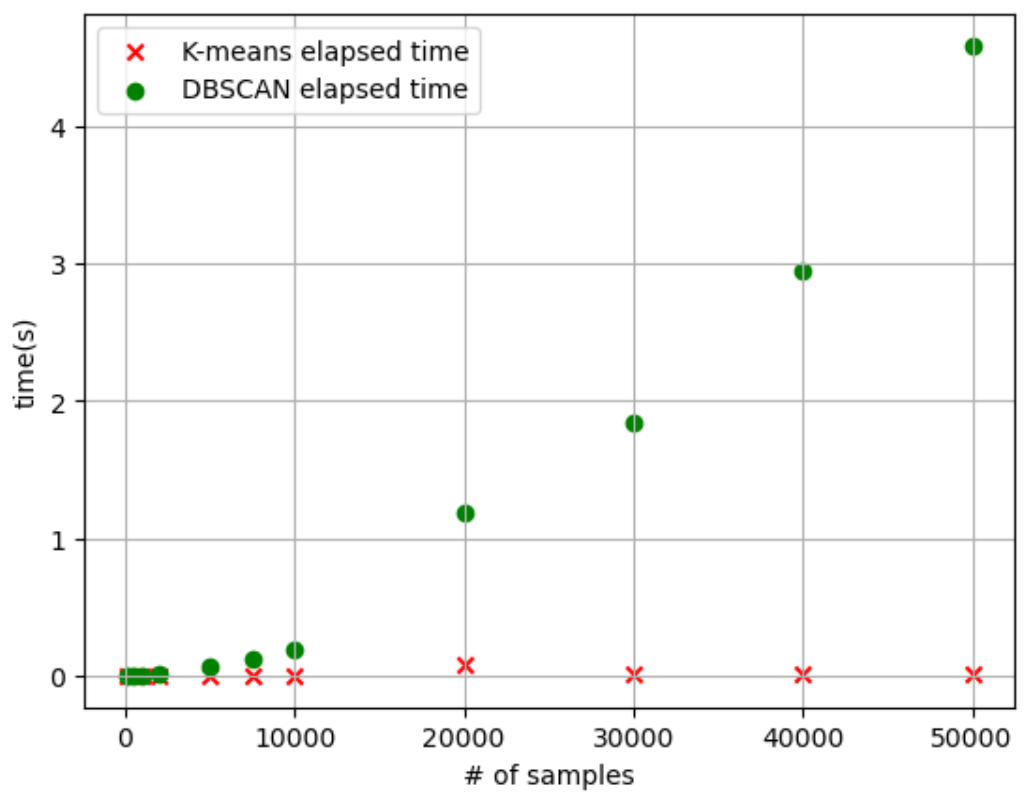
K-means와 클러스터링 소요 시간을 비교하면?
- 데이터의 수가 적을 때는 K-means 알고리즘의 수행 시간이 DBSCAN에 비해 더 길었으나, 군집화할 데이터의 수가 많아질수록 DBSCAN의 알고리즘 수행 시간이 급격하게 늘어난다.
2. 느낀 점, 어려웠던 점
먼저, Pytorch에 익숙하지 않다보니, 실습 코드를 읽는 데 어려움이 있었다. GPT의 도움을 받아 해석했는데, 내용 역시 쉽지 않았다. 그나마 다행인 건 학교에서 배웠던 개념들이라 학교 자료를 찾아보며 공부해서 이해하는 데 어려움은 크게 없었다. 오늘부터 퀘스트가 아니더라도 평소에 공부하는 코드들을 깃헙의 새 레포에 올리기 시작했다.
반응형
'AI > ML' 카테고리의 다른 글
| [10/2] 아이펠 리서치 15기 TIL | Loss F, Activation F, Optimizer (0) | 2025.10.12 |
|---|---|
| [10/1] 아이펠 리서치 15기 TIL | ML 학습 방법론, ML 아키텍처, MLOps (0) | 2025.10.09 |
| [9/24] 아이펠 리서치 15기 TIL | Evaluation Matric (0) | 2025.09.24 |
| [9/23] 아이펠 리서치 15기 TIL | Git & Github 튜토리얼 (1) | 2025.09.23 |
| [9/19] 아이펠 리서치 15기 TIL | 온보딩 퀘스트 (Generative Agents 논문 분석) (1) | 2025.09.19 |


