반응형
1. 오늘 배운 내용
오늘은 판다스를 이용한 기초적인 데이터 전처리와 모델 평가 척도를 배웠다.
이번 노드에서 총 6가지의 데이터 전처리 방법을 배웠다.
- 결측치
- 중복 데이터
- 이상치
- 정규화 & 표준화
- 원-핫 인코딩
- 구간화
하지만 이번 포스팅은 모델 평가 척도에 대해 다룰 것이다.
목차
1. Loss & Metric
2. Confusion Matrix & Precision/Recal
3. Precision-Recall 커브 & ROC 커브
4. 회귀모델의 평가척도
1. Loss & Metric
- Loss : 모델 학습시 학습데이터(train data) 를 바탕으로 계산되어, 모델의 파라미터 업데이트에 활용되는 함수
- Metric : 모델 학습 종료 후 테스트데이터(test data) 를 바탕으로 계산되어, 학습된 모델의 성능을 평가하는데 활용되는 함수
Metric 함수를 Loss 로 사용하면 안되는 이유
- 대부분의 Metric 함수는 불연속이라서 미분이 불가능함 → 경사하강법 사용 불가
- 과적합(overfitting) 문제 발생 → train 데이터에만 맞게 학습되어서 test 데이터에서는 낮은 성능을 보임
- 값이 크게 변동하는 경향이 있음 → 최소값이 아닌 극소값에 도달하거나 발산할 가능성이 있음
- 이런 이유들로 인해 보통 MSE나 cross-entropy를 loss 함수로 사용함
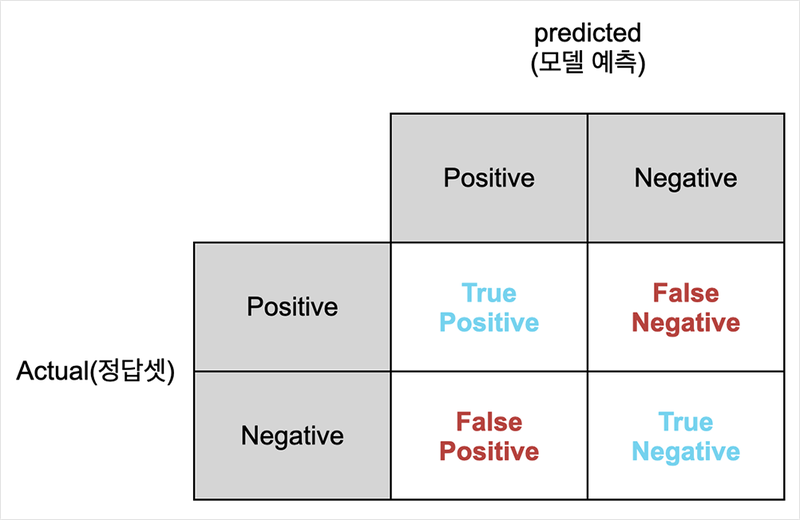
2. Confusion Matrix & Precision/Recal
- True Positive (TP) - 모델이 양성(Positive)을 양성으로 맞혔을 때
- True Negative (TN) - 모델이 음성(Negative)을 음성으로 맞혔을 때
- False Positive (FP) - 모델이 음성(Negative)을 양성(Positive)으로 잘못 예측했을 때
- False Negative (FN) - 모델이 양성(Positive)을 음성(Negative)으로 잘못 예측했을 때
- 정확도(Accuracy) = (TP + TN) / (TP + TN + FN + FP)
- 정밀도(Precision) = TP / (TP + FP) → 모델이 Positive라고 예측한 것들 중 실제로 Positive인 비율
- 재현율(Recall) = TP / (TP + FN) → 실제 Positive인 것들 중 모델이 Positive라고 예측한 비율
F-score
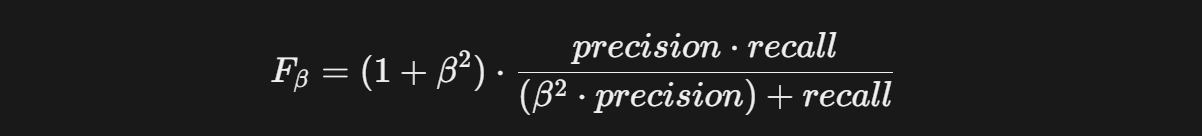
여기서 beta = 1일 경우 F1-score 라고 한다.
- Precision을 더 중요시 → beta > 1
- Recall을 더 중요시 → beta < 1
3. Precision-Recall 커브 & ROC 커브
(1) PR 커브(Precision-Recall Curve)
- Recall을 X축, Precision을 Y축에 놓고 Threshold 변화에 따른 두 값의 변화를 그래프로 그린 것
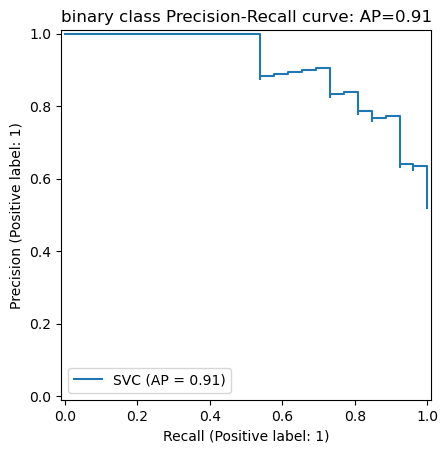
- 그래프 아래쪽의 면적을 구한 것이 PR AUC(Area Under Curve)
- sklearn 패키지의 average_precision_score사용해서 구할 수 있다.
(2) ROC 커브(Receiver Operating Characteristic Curve)
- Confusion Matrix 수치를 활용해, 분류기의 분류 능력을 그래프로 표현하는 방법
- X축은 TPR(Sencitivity), Y축은 FPR(1 - Specificity)로 구성
- TPR = TP / (TP + FN)
- FPR = FP / (TN + FP)

- 점선이 ROC이고, 그 밑 영역은 AUC
- AUC의 넓이가 클수록 좋은 성능의 모델이다.
- sklearn 패키지의 roc_curve 와 auc 함수를 사용해 커브를 그리고 AUC를 구할 수 있다.
- 이 곡선(ROC)이 대각선에 가까울수록 무작위 성능에 가까워진다.
4. 회귀모델의 평가척도
- MSE(Mean Square Error), RMSE(MSE에 루트를 씌운 형태) 등 square 계열의 Metric
- MAE(Mean Absolute Error), MAPE(MAE를 백분율로 나타낸 것) 등 절대값 계열의 Metric
- 오차에 크기에 영향을 더 많이 받는 square 계열의 Metric이 이상치에 민감하다.

2. 느낀 점, 어려웠던 점
오늘 배운 내용들은 저번 시간과 다르게 생소한 것(Git)이 아니라 학교 전공으로 배웠던 경험이 있어서 비교적 수월하게 진행할 수 있었다. 하지만 Confusion Matrix(혼동 행렬)의 경우는 몇 번을 해도 할 때마다 헷갈린다. 용어가 착착 붙지 않아서 그런 것 같다. 노드 후반에 다양한 ML모델의 평가척도(회귀모델, 생성형 이미지, 추천시스템 등)을 소개하는 글을 읽었는데, 이것들은 처음 보는 것들이라 재미있었다.
반응형
'AI > ML' 카테고리의 다른 글
| [10/2] 아이펠 리서치 15기 TIL | Loss F, Activation F, Optimizer (0) | 2025.10.12 |
|---|---|
| [10/1] 아이펠 리서치 15기 TIL | ML 학습 방법론, ML 아키텍처, MLOps (0) | 2025.10.09 |
| [9/25] 아이펠 리서치 15기 TIL | Regularization(Lasso, Ridge) & Clustering(K-means, DBSCAN) (0) | 2025.09.25 |
| [9/23] 아이펠 리서치 15기 TIL | Git & Github 튜토리얼 (1) | 2025.09.23 |
| [9/19] 아이펠 리서치 15기 TIL | 온보딩 퀘스트 (Generative Agents 논문 분석) (1) | 2025.09.19 |


