데이콘의 결측치 보간 챌린지 데이터를 사용하여 결측치를 보간하는 여러 가지 방법에 대해 알아보겠습니다.
# 패키지 세팅
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.impute import SimpleImputer, KNNImputer
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
# 데이터 로드
data = pd.read_csv('/content/drive/MyDrive/Colab Notebooks/공모전/data.csv')
df = pd.DataFrame(data['Value'], columns=['Value'])
df
이 데이터는 일정한 텀 마다 센서에서 온도를 측정한 일변량 시계열 데이터이며, 이 과정에서 기기/통신 결함으로 인한 결측이 발생한 상태입니다.
# 결측치 확인
df.info()
print('\nMissing Value :')
df.isna().sum()
데이터의 타입은 float64 형태이고 결측치의 개수는 총 22493개입니다.
이제 결측치를 포함한 데이터를 시각화 해보겠습니다.
# 결측치 포함 데이터 시각화
plt.figure(figsize = (15, 8))
sns.lineplot(data=df, marker='o')
plt.title('Original Data')
plt.show()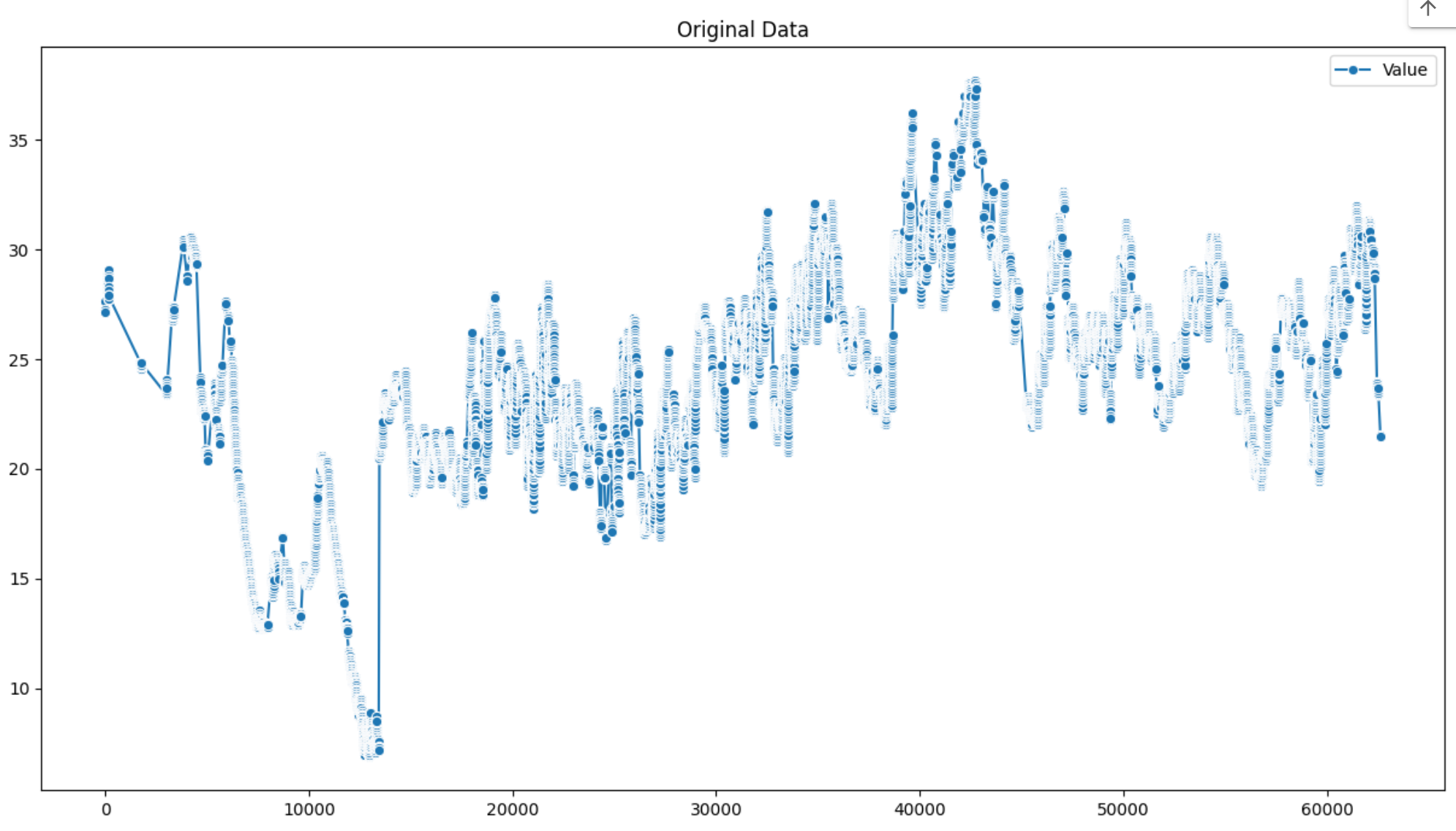
데이터의 일정 구간마다 결측치가 포함되어 있는 것을 알 수 있습니다.
이제 각 보간법으로 결측치를 보간하겠습니다.
# 1. 1차 선형보간법
df_linear = df.interpolate(mathod = 'linear')
# 2. 2차 선형보간법
df_quadratic = df.interpolate(method = 'quadratic')
# 3. 평균대치법
imputer_mean = SimpleImputer(strategy = 'mean')
df_mean = imputer_mean.fit_transform(df)
df_mean = pd.DataFrame(df_mean, columns = ['Value'])
# 4. 0값으로 대체
df_zero = df.fillna(0)
# 5. KNN 방법
imputer_knn = KNNImputer(n_neighbors=3)
df_knn = imputer_knn.fit_transform(df)
df_knn = pd.DataFrame(df_knn, columns = ['Value'])
# 6. MICE 다중대치법
mice_imputer = IterativeImputer()
df_mice = mice_imputer.fit_transform(df)
df_mice = pd.DataFrame(df_mice, columns = ['Value'])
# 결측치 보간 결과
miss_df = pd.DataFrame({
'Linear': df_linear.iloc[:].reset_index(drop=True)['Value'],
'Quadratic': df_quadratic.iloc[:].reset_index(drop=True)['Value'],
'Mean': df_mean.iloc[:].reset_index(drop=True)['Value'],
'Zero': df_zero.iloc[:].reset_index(drop=True)['Value'],
'KNN': df_knn.iloc[:].reset_index(drop=True)['Value'],
'MICE': df_mice.iloc[:].reset_index(drop=True)['Value']})
miss_df
1차 선형보간법은 두 점 사이의 값을 직선으로 추정하는 방법입니다. 이 방법은 주어진 두 점 사이의 직선 방정식을 이용하여 두 점 사이의 임의의 점의 값을 추정합니다.
장점
- 간단함: 계산이 매우 간단하고 이해하기 쉽습니다.
- 빠름: 계산 속도가 빠르며 대규모 데이터에도 적용하기 용이합니다.
- 연속성: 데이터 포인트 사이의 값이 연속적으로 변화합니다.
- 적용 범위: 다양한 분야에 널리 사용되며, 기초적인 데이터 보간에 적합합니다.
단점
- 정확성 부족: 데이터의 실제 변화가 선형이 아닌 경우, 특히 곡선형 패턴이 있는 경우 부정확할 수 있습니다.
- 매끄럽지 않음: 데이터의 변동이 급격한 경우, 보간된 값이 매끄럽지 않고 갑작스럽게 변화할 수 있습니다.
- 복잡한 데이터: 비선형 데이터의 경우, 1차 보간법은 복잡한 패턴을 제대로 반영하지 못합니다.
2차 선형보간법은세 개의 데이터 포인트를 사용하여 2차 다항식을 통해 중간 값을 추정하는 방법입니다. 이 방법은 1차 선형보간법보다 복잡하지만 곡선형 데이터를 더 정확하게 추정할 수 있습니다.
장점
- 정확성: 데이터가 선형이 아닌 경우에도 더 높은 정확도를 제공합니다. 곡선형 패턴을 더 잘 반영합니다.
- 매끄러움: 보간된 값이 더 매끄럽고, 데이터의 급격한 변화를 더 자연스럽게 반영할 수 있습니다.
- 적응성: 데이터의 패턴이 약간 복잡한 경우에도 비교적 잘 적응합니다.
단점
- 복잡성: 계산이 1차 보간법보다 복잡합니다.
- 계산 비용: 계산 속도가 상대적으로 느리며, 대규모 데이터에서는 계산 비용이 증가할 수 있습니다.
- 오버피팅: 데이터 포인트가 적을 때는 실제 데이터 패턴보다 더 복잡한 형태를 만들어내는 경향이 있어 오버피팅이 발생할 수 있습니다.
- 경계 문제: 데이터의 시작과 끝에서 경계 조건을 설정하는 것이 어려울 수 있습니다.
평균대치법이란 결측치를 처리하는 가장 간단하고 흔히 사용되는 방법 중 하나입니다. 이 방법에서는 결측값을 해당 열(변수)의 평균값으로 대체합니다. 여기서는 sklearn이 제공하는 simpleimputer를 사용합니다.
장점
- 간단함: 계산이 간단하고 이해하기 쉽습니다.
- 빠름: 대규모 데이터셋에서도 빠르게 적용할 수 있습니다.
- 데이터 보존: 결측치가 채워지므로 데이터의 크기가 줄어들지 않습니다.
단점
- 분산 감소: 모든 결측치를 평균으로 대체하기 때문에 데이터의 분산이 감소하고, 결과적으로 데이터의 변동성을 왜곡할 수 있습니다.
- 상관관계 왜곡: 다른 변수들과의 상관관계를 왜곡할 수 있습니다.
- 편향: 데이터가 편향될 수 있으며, 분석 결과에 부정적인 영향을 미칠 수 있습니다.
KNN 알고리즘이란 데이터의 유사성을 기반으로 분류하는 대표적인 머신러닝 기법입니다. 새로운 데이터의 특성이 기존 데이터와 얼마나 유사한지를 측정하여, 가장 유사한 k개의 데이터를 찾고, 이를 바탕으로 새로운 데이터의 분류를 예측합니다.
장점
- 간단하고 이해하기 쉬운 알고리즘
- 수치형 데이터에 대해 높은 정확도를 보입니다
단점
- 연산 속도가 느립니다
- 데이터의 편향성, 이상치에 민감한 특성이 있습니다.
MICE 다중대치법이란 결측치 처리를 위한 대표적인 다중대치법 기법입니다. 결측치가 있는 변수 이외의 다른 변수들까지 함께 고려하여 결측치를 추정합니다.
장점
- 연속형, 범주형 등 다양한 데이터 유형에 적용 가능합니다.
- 불확실성을 고려하여 여러 개의 대체값을 생성합니다.
단점
- 대체 모델 선택, 반복 횟수 등 하이퍼파라미터 튜닝이 필요합니다.
- 대체 모델의 성능에 따라 결과가 달라질 수 있습니다.
KNN 알고리즘과 MICE 다중대치법을 비교하자면,
KNN 알고리즘은 간단하고 이해하기 쉬운 분류 모델이지만 연산 속도와 데이터 편향성에 취약한 편입니다.
반면 MICE 다중대치법은 결측치 처리에 효과적이지만 모델 선택 및 하이퍼파라미터 튜닝이 필요합니다.
그러므로 사용 목적과 데이터 특성에 따라 적절한 기법을 선택해야 합니다.
이제 시각화를 해보겠습니다.
fig, axes = plt.subplots(7, 1, figsize = (15, 60))
sns.lineplot(data = df, marker='o', ax = axes[0], legend = 'auto')
axes[0].set_title('Original Data')
sns.lineplot(data=df_linear , marker='o', ax=axes[1], legend='auto')
axes[1].set_title('Linear Data')
sns.lineplot(data=df_quadratic , marker='o', ax=axes[2], legend='auto')
axes[2].set_title('Quadratic Data')
sns.lineplot(data=df_mean , marker='o', ax=axes[3], legend='auto')
axes[3].set_title('Simple Mean')
sns.lineplot(data=df_zero , marker='o', ax=axes[4], legend='auto')
axes[4].set_title('Zero')
sns.lineplot(data=df_knn , marker='o', ax=axes[5], legend='auto')
axes[5].set_title('df_knn')
sns.lineplot(data=df_mice , marker='o', ax=axes[6], legend='auto')
axes[6].set_title('df_mice')



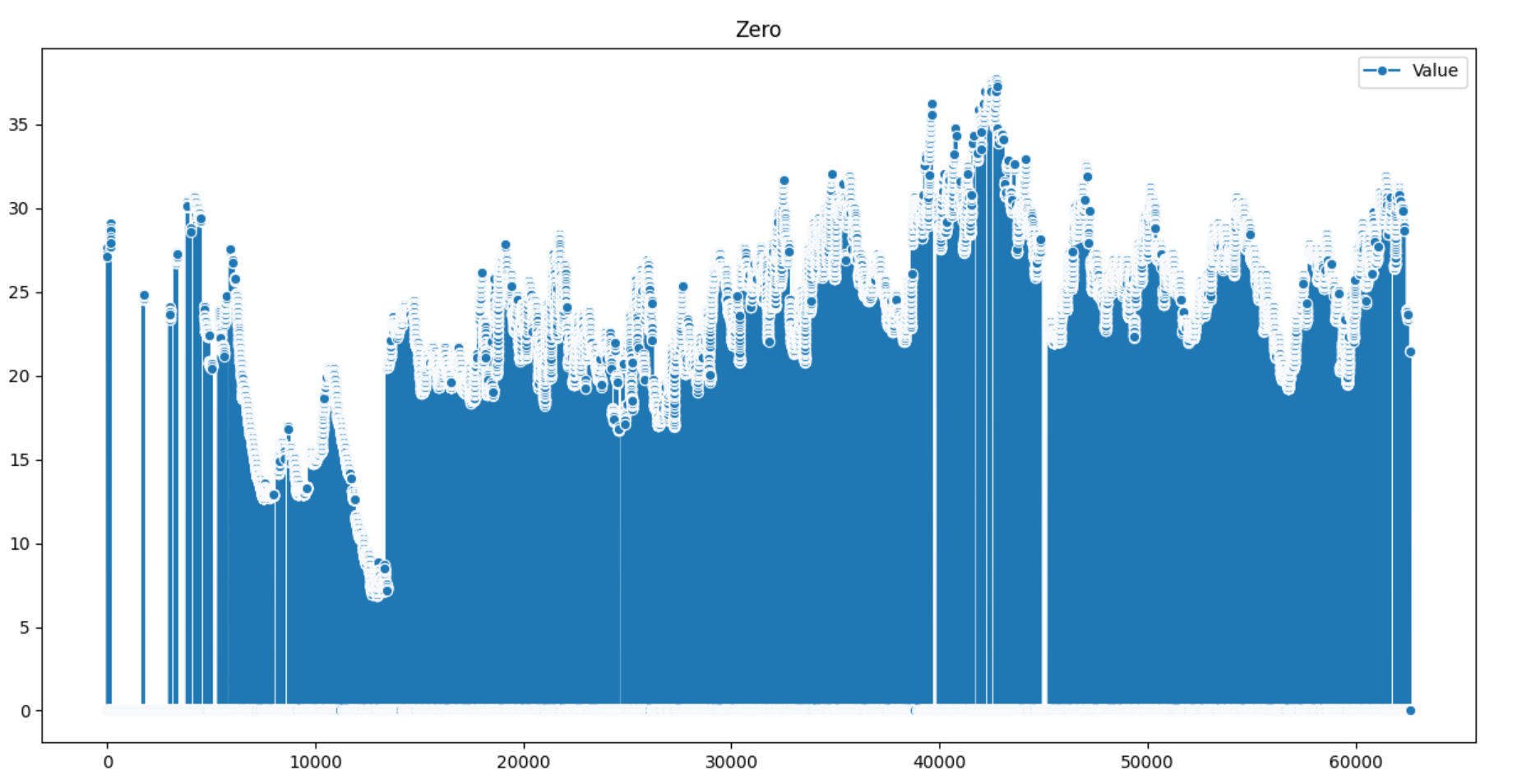


이 데이터에서는 평균대치법, KNN 알고리즘, MICE 다중대치법 모두 거의 동일한 결과를 얻을 수 있다는 사실을 알 수 있습니다.
이제 1차 선형보간법으로 보간한 그래프와 원본 데이터를 비교해보겠습니다.
# 원본 데이터와 new 데이터 비교
plt.figure(figsize=(9,3))
plt.subplot(1,2,1)
plt.plot(df["Value"])
plt.subplot(1,2,2)
plt.plot(miss_df["Linear"], c='g')
plt.show()
이번 포스팅에서는 제 1차 선형보간법을 이용해 결측치를 보간한 데이터를 시각화까지 해보았습니다.
이 데이터의 경우, 단순 일변량 시계열 데이터이기 때문에 평균대치법, KNN, MICE 방법들을 이용한 결과가 서로 큰 차이가 없는 것으로 나왔습니다.
타 다변량 데이터의 경우, 각각의 데이터 특성에 따라 그에 맞는 방법을 이용하여 보간해야 할 것입니다.
'Python' 카테고리의 다른 글
| [Python] 이커머스 데이터 퍼널 분석(Funnel Analysis) (0) | 2025.02.16 |
|---|---|
| [Python] 이커머스 고객 세분화 분석 (RFM, 코호트 분석) (0) | 2025.02.09 |
| [Python] 이상치 탐지 기법 (IQR, Isolation Forest, rolling 함수, decompose 패키지) (0) | 2024.05.11 |


