이상치란?
전체 데이터의 대부분의 패턴, 범위에서 크게 벗어난 값인데 아주 작은 값일 수 있고, 아주 큰 값일 수 있습니다.
이상치를 중요하게 바라봐야 하는 이유는?
극단적인 값으로 인해 통계치 또는 ML 학습에서 영향을 받게 되기 때문입니다.
도메인의 영향
이상치는 도메인에 따라, 이상치 탐지 기법에 따라 다를 수 있기 때문에 도메인의 영향을 받습니다.
이번 포스팅에서는 임의로 이상치가 포함된 데이터셋을 만들고, 여러 방법을 사용한 이상치 탐지 기법을 알아보겠습니다.
먼저 이상치 탐지에 필요한 패키지를 로드합니다.
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 이상치 탐지 방법
from sklearn.ensemble import IsolationForest
from sklearn.datasets import make_blobs
이상치를 포함한 데이터를 생성합니다.
# 데이터 생성
data = np.random.randn(100) * 20 + 50
data = np.append(data, [150, -50, 200]) # 명확한 이상치
# 데이터프레임으로 변환
df = pd.DataFrame(data, columns=['Data'])
df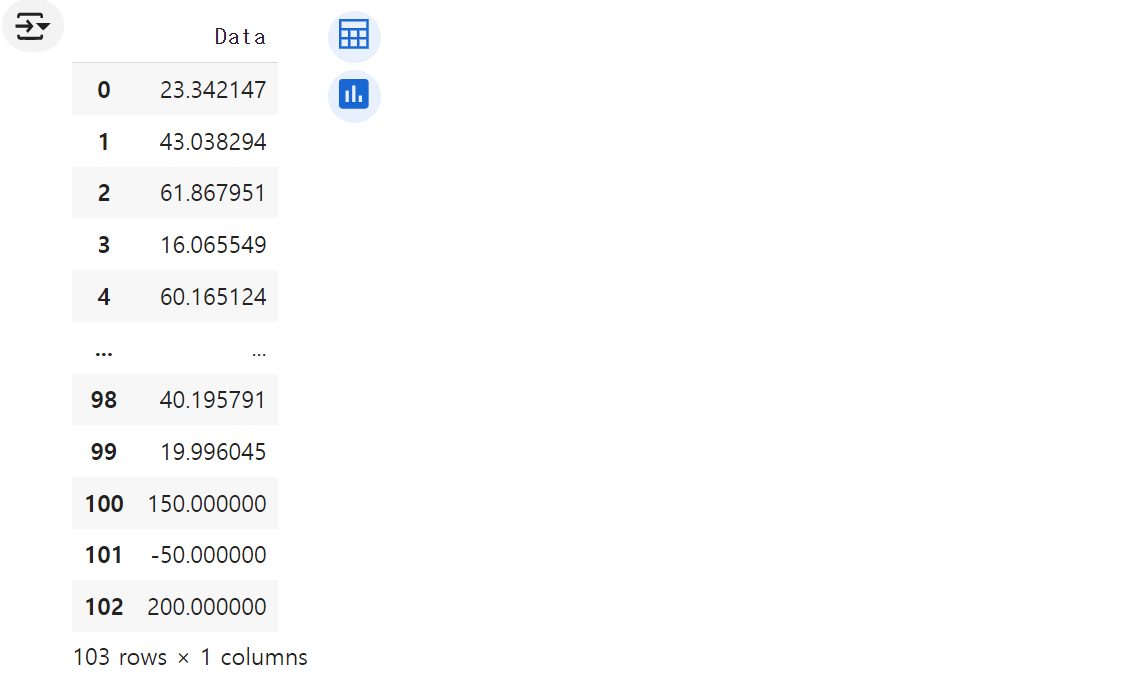
1. IQR
# Q1, Q3 계산
Q1 = df['Data'].quantile(0.25)
Q3 = df['Data'].quantile(0.75)
# IQR
IQR = Q3 - Q1
# 이상치의 경계 계싼
lower_bound = Q1 - 1.5*IQR
upper_bound = Q3 + 1.5*IQR
# 이상치 식별
outliers = df[(df['Data'] < lower_bound) | (df['Data'] > upper_bound)]
outliers
통계학에서 흔히 사용되는 IQR을 사용한 방법입니다.

2. Isolation Forest
Isolation Forest는 기본적으로 데이터셋을 의사결정나무 형태로 표현한 다음, 정상값을 분류하기 위해서는 의사결정나무를 깊숙하게 타고 내려가야 하는 반면, 이상치는 의사결정나무의 비교적 상단부에서 분류할 수 있다는 점을 이용해 이상치를 탐지하는 기법입니다.
이러한 특성을 이용해 의사결정나무를 몇 회 타고 내려가야 고립되는지를 기준으로 정상값과 이상치를 구분합니다.
코드로 알아보겠습니다.
# 중심점이 3개인 데이터 생성
data, _ = make_blobs(n_samples=300, centers=3, random_state=111)
# 이상치 추가
outliers = np.random.uniform(low=-10, high=10, size=(20,2))
# 위의 원본 데이터와 이상치 데이터 합치기
data = np.vstack([data, outliers])
# Isolation Forest로 모델 생성 및 학습
model = IsolationForest(n_estimators=100, contamination=0.5, random_state=111)
# 이상치가 차지하는 비율을 나타낸 것
# 0과 1 사이의 실수로 표현, 기본은 'auto' -> 데이터셋에 따라 알아서 이상치를 탐지.
# 값이 높아질수록 더 많은 데이터를 이상치로 간주하게 됨. False Positive가 증가하는 경우
# 값이 낮은 경우는 이상치로 판단되는 데이터 포인트 수가 줄어듦. False Negative가 증가하는 경우
# 모델이 직접 예측
predictions = model.fit_predict(data)
# 데이터 시각화 진행
plt.figure(figsize=(10,6))
plt.scatter(data[:, 0], data[:, 1], c = predictions, cmap='Paired', marker='o', s=30, edgecolor='k')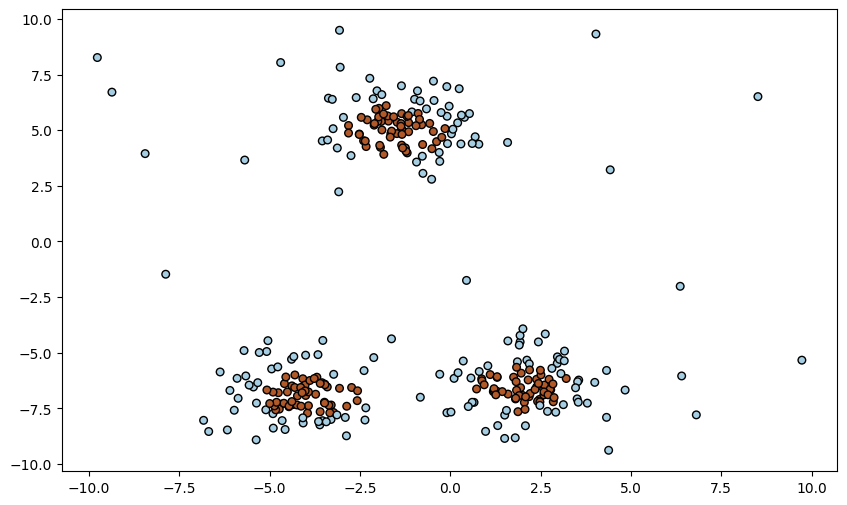
3. 시계열 데이터와 rolling 함수
rolling 함수는 시계열 데이터를 이동하면서 이동 평균, 이동 합계, 이동 표준 편차 등의 통계량을 계산하는 데 사용됩니다.
# 데이터 생성
np.random.seed(111)
data = np.random.randn(100).cumsum() + 100
# 이상치 추가
data[20] += 50
data[70] -= 30
data[50] += 15
# 이동 평균, 이동 표준 편차 계산으로 이상치 탐지
window_size = 5
moving_average = pd.Series(data).rolling(window = window_size).mean()
moving_std = pd.Series(data).rolling(window = window_size).std()
# 이상치 탐지 기준 설정 (평균 +- 1.5 * 표준편차)
upper_bound = moving_average + 1.5 * moving_std
lower_bound = moving_average - 1.5 * moving_std
# 데이터프레임을 생성해서 확인하기
df = pd.DataFrame({'Data':data, 'Moving Average':moving_average, 'upper_bound':upper_bound, 'lower_bound':lower_bound})
# 이상치 탐지
outliers = df[(df['Data'] > df['upper_bound']) | (df['Data'] < df['lower_bound'])]
# 시각화로 확인해 보기
plt.figure(figsize=(12,9))
plt.plot(df['Data'], label='Data', color='gray', marker='o', markersize=4, linestyle='-')
plt.plot(df['Moving Average'], color='red', label='Moving average')
plt.fill_between(df.index, df['upper_bound'], df['lower_bound'], color='gray', alpha=0.2, label='Confidence Interval')
plt.scatter(outliers.index, outliers['Data'], color='magenta', label='Outliers', s=200, edgecolor='black', zorder=5)
plt.show()
4. decompose 패키지
decompose 패키지를 사용해 시계열 데이터를 분해하고, 추세와 계절성 및 잔차 그래프로 이상치를 탐지할 수 있습니다.
from statsmodels.tsa.seasonal import seasonal_decompose
# 시계열 분해
result = seasonal_decompose(data, model='additive', period=4)
result.plot()
# 잔차를 통한 이상치 탐지
residuals = result.resid
outliers = residuals[abs(residuals) > 2 * residuals.std()]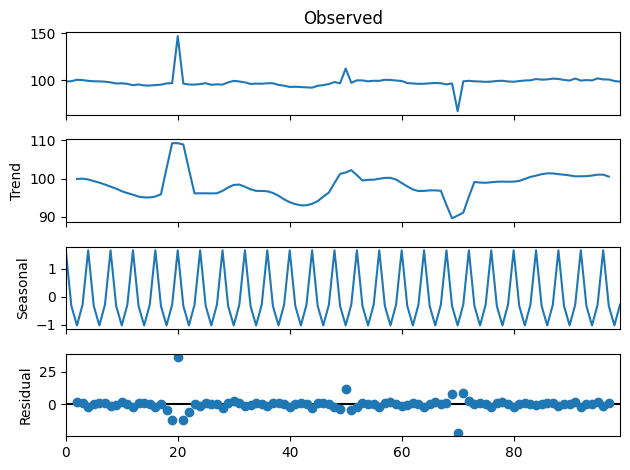
Seasonal(계절성) 그래프에서의 특이사항은 없지만 Trend(추세)와 Residual(잔차) 그래프에서는 이상치가 명확하게 보이는 것을 알 수 있습니다.
'Python' 카테고리의 다른 글
| [Python] 이커머스 데이터 퍼널 분석(Funnel Analysis) (0) | 2025.02.16 |
|---|---|
| [Python] 이커머스 고객 세분화 분석 (RFM, 코호트 분석) (0) | 2025.02.09 |
| [Python] 결측치 보간법 (1/2차 선형보간법, 평균대치법, KNN, MICE) (0) | 2024.05.29 |


