[통계] 상대위험도(RR)와 오즈비(OR)의 신뢰구간 (with R)

이전 포스팅: 오즈와 상대위험도의 개념

https://choiwonjin.tistory.com/43

[통계] 오즈(odds), 상대위험도(RR) + 유의성 검정 (with R)

---

상대위험도와 오즈비는 단순한 점 추정치이다.

따라서, 이를 보완하기 위해 신뢰구간을 제시할 수 있다.

 

그런데, 상대위험도와 오즈비는 정규분포를 따르지 않는다.

하지만 자연 로그를 취한 표본 상대위험도와 표본 오즈비가 근사적으로 정규분포를 따른다는 것을 이용하여 신뢰구간을 구할 수 있다(중심극한정리 참고).

2차원 분할표의 일반적인 형태

• 위험요인에 노출 시 사건발생확률 $\widehat{\pi}_1$ = $p_1$ = $n_{11}$/$n_{1+}$
• 위험요인에 미노출 시 사건발생확률 $\widehat{\pi}_2$ = $p_2$ = $n_{21}$/$n_{2+}$

---

1. 상대위험도의 신뢰구간

로그-상대위험도는 근사적으로 정규분포를 따른다.

 

이 때, 델타 메소드(delta method)란?

간단히 말하면, 매끄럽게 변하는 함수가 점근적으로 정규성을 띠는 추정량의 함수일 경우, 해당 함수도 점근적으로 정규 분포를 따른다는 것인데, 수식으로 표현하면 아래와 같다.

delta method

 

이제, 위의 사실을 이용해 log(RR)의 분산 추정치를 구할 수 있다.

여기서, 두 변수는 독립을 가정하기 때문에 공분산은 0이다.

 

마지막으로, $\log (RR)$에 관한 $100(1-\alpha)%$ 신뢰구간은 아래와 같으며

 

$RR$에 관한 $100(1-\alpha)%$ 신뢰구간은 아래와 같다.

---

이제, 저번 포스팅에서의 예시였던 아스피린, 플라시보 데이터를 이용해 직접 계산해보면,

• $\widehat{RR} = \frac{139/11037}{239/11034} = 0.581$
• $\log \widehat{RR} = \log 0.581 = -0.543$
• $\widehat{Var}(\log \widehat{RR}) = \frac{1}{n_{11}} - \frac{1}{n_{1+}} + \frac{1}{n_{21}} - \frac{1}{n_{2+}} = 0.0112$
• $\widehat{SE}(\log \widehat{RR}) = \sqrt{0.0112} = 0.106$

$\log (RR)$에 관한 $100(1-\alpha)%$ 신뢰구간

$(log (0.58) - 1.96 \times 0.106, log (0.58) + 1.96 \times 0.106) = (-0.751, -0.335)$

 

$RR$에 관한 $100(1-\alpha)%$ 신뢰구간

$(e^{-0.751}, e^{-0.335}) = (0.472, 0.715)$

 

해석:

$RR$의 95% 신뢰구간 $ (0.472, 0.715) $가 1을 포함하지 않으므로 5% 유의수준에서 아스피린과 플라시보를 복용한 두 그룹의 심근경색 위험률에는 유의미한 차이가 있음을 알 수 있다.

(1을 포함한다는 의미는 상대위험도 $= 1$일 수 있다는 의미를 포함한다는 것인데, 이는 두 그룹간에 차이가 없음을 나타낸다.)

 

유의성 검정까지 한다면?

$H_0: RR = 1$ vs $H_1: RR \neq 1$

$\Leftrightarrow H_0: \log (RR) = 0$ vs $H_1: \log (RR) \neq 0 $

 

검정통계량

$Z = \frac{ \log (\widehat{RR}) - 0}{\widehat{se}(\log(\widehat{RR}))} = -5.12$

2*(pnorm(-5.12)) # 3.055357e-07

유의하다.

 

R에서 epitab 함수 사용

table<-matrix(c(139,239,10898,10795),nrow=2)
dimnames(table)=list(Group=c("Aspirin","Placebo"),MI=c("Yes","No"))

library(epitools)
epitab(table, method='riskratio', rev='both')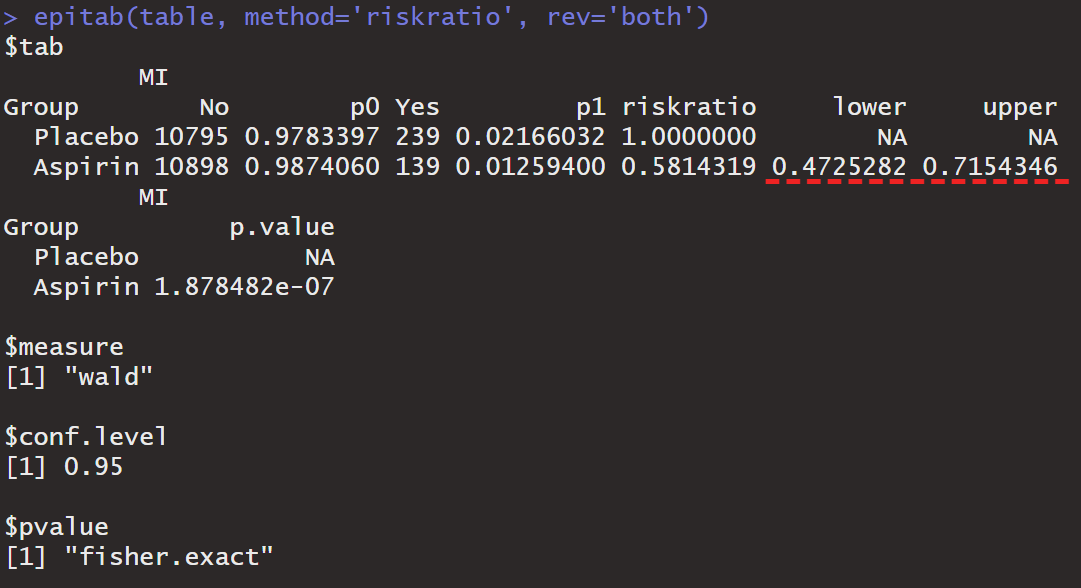

---

2. 오즈비의 신뢰구간

 

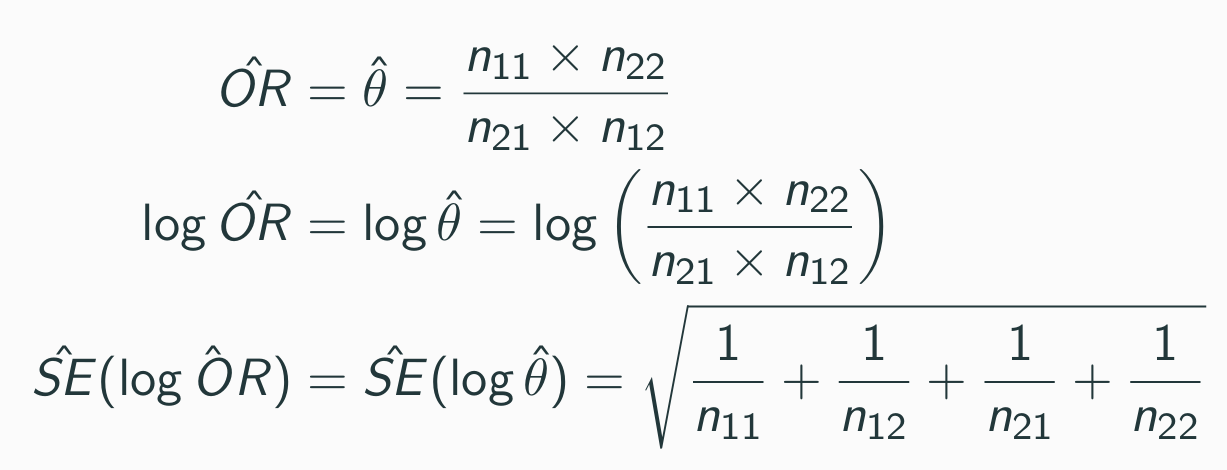
아스피린, 플라시보 데이터로 추정치를 구해보면

 

• $\hat{\theta} = \frac{139 \times 10795}{239 \times 10898} = 0.576$
• $\log \hat{\theta} = -0.552$
• $\widehat{Var}(\log \widehat{\theta}) = 0.01$
• $\widehat{SE}(\log \widehat{\theta}) = \sqrt{0.01} = 0.108$

$\log (\theta)$에 관한 $100(1-\alpha)%$ 신뢰구간

$(log (0.576) - 1.96 \times 0.108, log (0.576) + 1.96 \times 0.108) =  (-0.764, -0.340)$

 

$\theta$에 관한 $100(1-\alpha)%$ 신뢰구간

$(e^{-0.764}, e^{-0.340}) = (0.466, 0.712)$

 

해석:

오즈비의 신뢰구간이 1을 포함하지 않으므로 5%의 유의수준에서 두 그룹의 심근경색 오즈에 차이가 있다.

 

유의성 검정

$H_0: \theta = 1$ vs $H_1: \theta \neq 1$

$\Leftrightarrow H_0: \log (\theta) = 0$ vs $H_1: \log (\theta) \neq 0 $

 

검정통계량

$Z = \frac{ \log (\widehat{\theta}) - 0}{\widehat{se}(\log(\widehat{\theta}))} = -5.11$

2*pnorm(-5.11) # 3.221588e-07

유의하다.

 

R에서 epitab 함수 사용

library(epitools)
epitab(table, method='oddsratio', rev='both')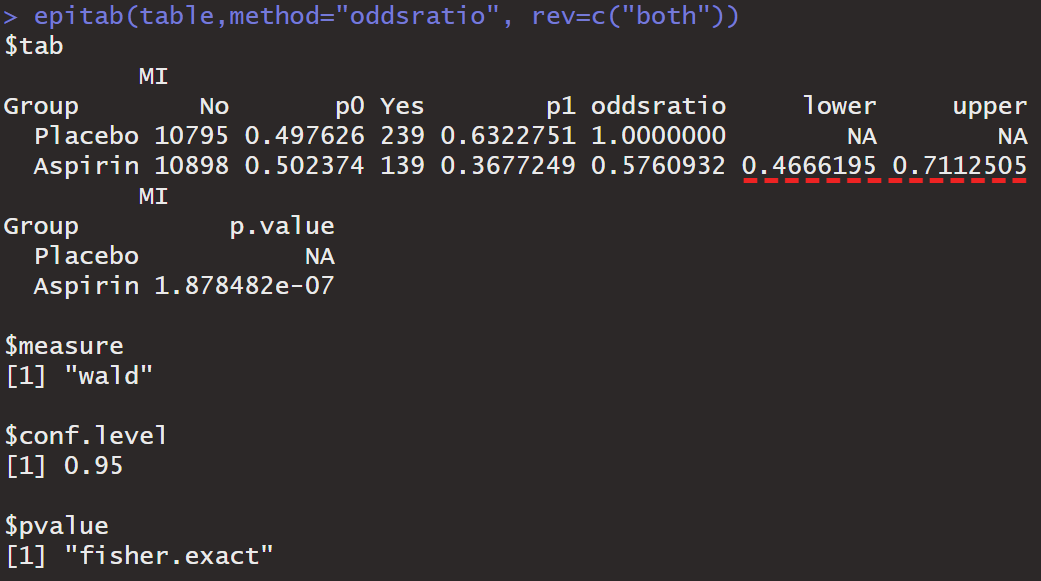

---

다음 포스팅: 연관성 검정

---

referance

단국대학교 통계데이터사이언스학과 이미성 교수님