R의 내장 데이터셋인 diamonds 데이터를 기반으로 하여 가설을 세우고 분석하는 프로젝트를 진행했습니다.

먼저 diamonds 데이터셋 소개를 하겠습니다.

diamonds 데이터셋은 ggplot2 패키지에 속해 있습니다.
library(ggplot2)
diamonds = as.data.frame(diamonds)
dim(diamonds)
head(diamonds)
str(diamonds)
summary(diamonds)

총 53940개의 관측치, 10개의 변수로 구성되어 있는 것을 알 수 있습니다.

총 10개의 변수 중 문자형 변수와 숫자형 변수는 각각 3개, 7개입니다.
이번 프로젝트에서 설정한 가설은 총 3개로 다음과 같습니다.
- 다이아몬드의 가격 분포는 시각적 특성(cut, color, clarity)에 따라 다르게 나타난다.
- 다이아몬드는 특정 속성들에 따라 몇 가지 군집으로 나눌 수 있다.
- 다이아몬드의 물리적 특성(carat, depth, table)과 시각적 특성(cut, color, clarity) 간에는 유의미한 상관 관계가 있다.
1. 다이아몬드의 가격 분포는 시각적 특성(cut, color, clarity)에 따라 다르게 나타난다.
분산분석을 이용해 분석해보겠습니다.
우선 검정할 3가지 변수의 독립여부를 판단하기 위해 다중공선성을 계산해보았습니다.
R프로그램상 다중공선성을 계산하기 위해서는 먼저 회귀분석을 시행해야 했기에,
다중회귀분석을 먼저 실시하고 다중공선성을 계산해보겠습니다.
library(ggplot2)
library(dplyr)
library(car)
# 다중 선형 회귀 분석 수행
model = lm(price ~ cut + color + clarity, data = diamonds)
# 회귀 분석 결과 요약
summary(model)
# 분산 팽창 계수 (VIF) 계산
vif_values = vif(model)
vif_values

그 결과, vif 값이 모두 10 이하가 나왔으므로 3개 변수가 모두 독립임을 알 수 있었습니다.
3개 변수가 독립이기 때문에 각각의 변수들이 가격에 미치는 영향을 따로 계산해야 했습니다.
이에 가장 최적화된 방법인 분산분석으로 분석을 해봤습니다.
#ANOVA 분석
anova_cut = aov(price ~ cut, data = diamonds)
summary(anova_cut)
anova_color = aov(price ~ color, data = diamonds)
summary(anova_color)
anova_clarity = aov(price ~ clarity, data = diamonds)
summary(anova_clarity)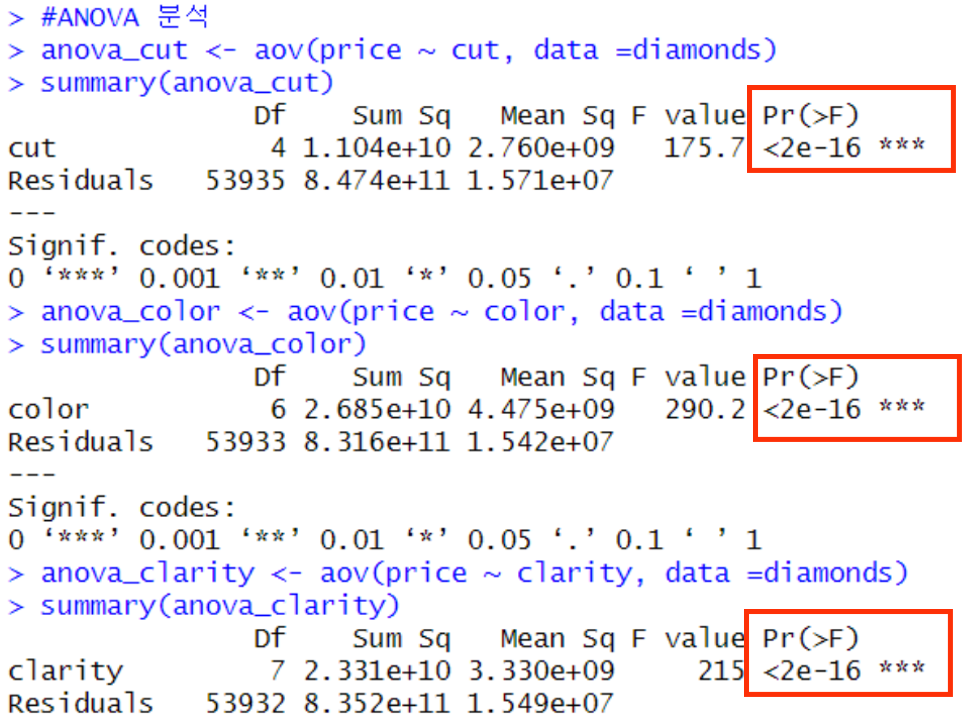
그 결과, 위 사진과 같이 p_value가 모두 매우 작게 나왔고, 이를 토대로 '다이아몬드의 가격 분포는 시각적인 특성에 따라 다르게 나타난다' 라는 결과를 얻었습니다.
해당 결과를 조금 더 세부적으로 확인해보기 위해 사후분석을 실시해보았습니다.
install.packages('agricolae')
library(agricolae)
scheffe.test(anova_cut, 'cut', alpha= 0.05, console= T)
scheffe.test(anova_color, 'color', alpha= 0.05, console= T)
scheffe.test(anova_clarity, 'clarity', alpha= 0.05, console= T)
왼쪽부터 차례대로 cut, color, clarity에 대한 사후분석 실행 결과입니다.
cut 변수의 사후분석 시행 결과, 유의수준 0.05에서 premium과 fair 그리고 very good과 good은 차이가 없으며, 사진에 색깔별로 표시해 둔 박스 간에는 유의수준 0.05에서 차이가 있음을 알 수 있었습니다.
나머지 color와 clarity에 대한 사후분석 또한 유의수준 0.05에서 박스 내의 등급에는 큰 차이가 없으며, 박스 간의 등급에는 차이가 있음을 알 수 있었습니다.
마지막으로 box-plot을 이용해 시각화를 해보겠습니다.
# cut 변수의 효과 시각화
ggplot(diamonds, aes(x = cut, y = price)) +
geom_boxplot(fill = "lightblue") +
labs(title = "다이아몬드 컷 품질에 따른 가격",
x = "컷 품질",
y = "가격 ($)") +
theme_minimal()
# color 변수의 효과 시각화
ggplot(diamonds, aes(x = color, y = price)) +
geom_boxplot(fill = "lightgreen") +
labs(title = "다이아몬드 색상에 따른 가격",
x = "색상",
y = "가격 ($)") +
theme_minimal()
# clarity 변수의 효과 시각화
ggplot(diamonds, aes(x = clarity, y = price)) +
geom_boxplot(fill = "lightcoral") +
labs(title = "다이아몬드 투명도에 따른 가격",
x = "투명도",
y = "가격 ($)") +
theme_minimal()

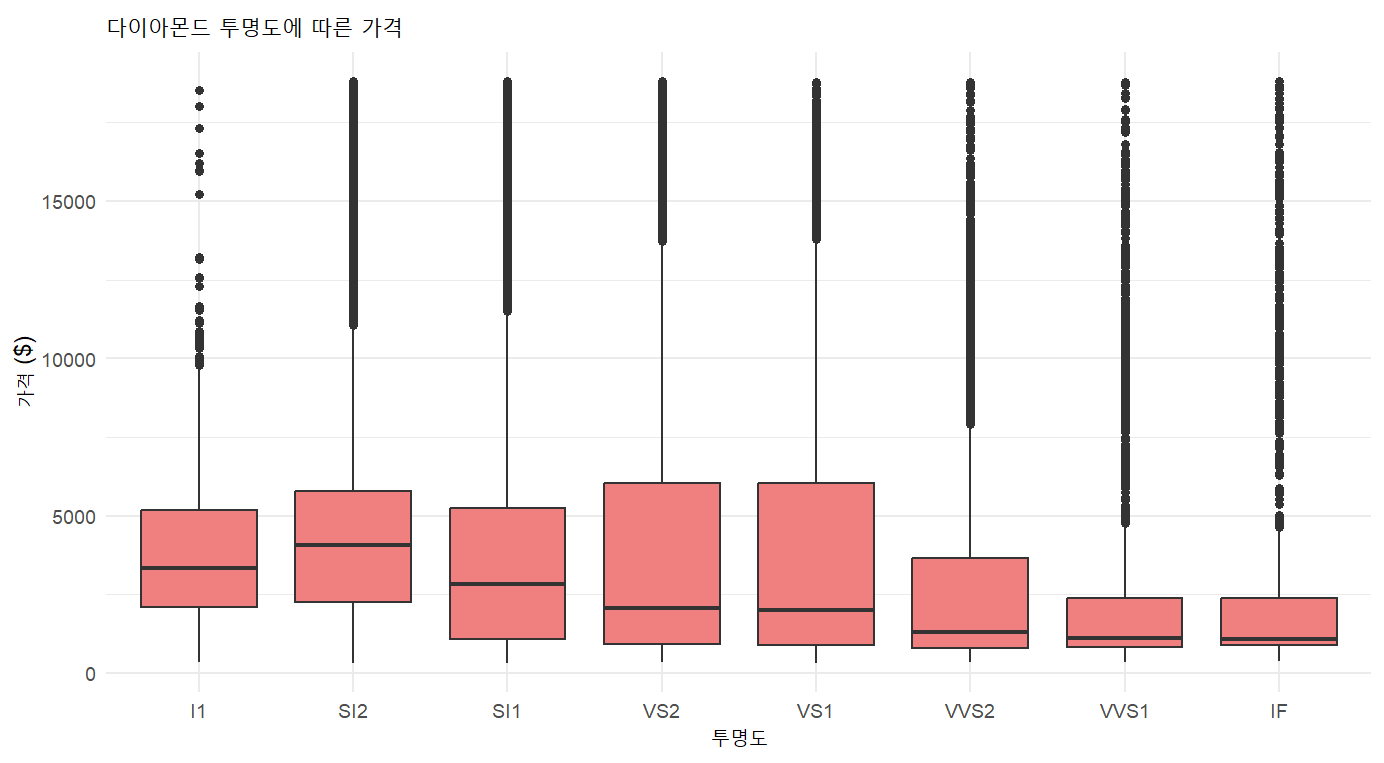
cut에 따른 가격 분포 그래프를 봤을 때, fair과 good에 차이가 크지 않긴 하지만, 앞서 분석한 사후분석 결과와 큰 차이 없이 나타나는 것을 확인할 수 있습니다.
결론
분산분석과 사후분석을 진행한 결과, 다이아몬드의 가격이 컷, 색상, 투명도에 따라 통계적으로 유의미하게 차이가 난다고 할 수 있습니다.
2. 다이아몬드는 특정 속성들에 따라 몇 가지 군집으로 나눌 수 있다.
이 가설에서는 주성분분석을 이용한 k-means 군집분석을 사용할 것입니다.
먼저 주성분분석을 시행하겠습니다.
# 패키지 로드
library(cluster)
library(factoextra)
# diamonds 데이터셋에서 숫자형 변수만 선택하고 표준화
diamonds_num = diamonds[, sapply(diamonds, is.numeric)]
diamonds_scaled = scale(diamonds_num)
# 주성분 분석 수행
pca_result = prcomp(diamonds_scaled, scale. = TRUE)
pca_result$rotation
# PCA 결과 요약 출력
summary(pca_result)

PC1, PC2의 로딩을 봤을 때,
PC1의 경우는 depth와 table을 제외한 모든 변수들의 적재가 유의미한 것으로 보이고,
PC2의 경우는 depth와 table 두 변수의 변동을 잘 설명한다는 것을 알 수 있습니다.

두 개의 주성분 만으로 전체 변수 변동의 86.4%를 설명할 수 있으므로, 성공적으로 차원을 축소했다고 할 수 있습니다.
이제 주성분분석 데이터를 기반으로 k-평균 군집분석을 시행하겠습니다.
# 첫 번째 두 개의 주성분만 선택하여 데이터 축소
pca_data = pca_result$x[, 1:2]
# k-평균 군집 분석 수행
set.seed(123)
kmeans_result = kmeans(pca_data, centers = 3, nstart = 20)
kmeans_result

k-평균 군집분석 결과 하단에 알 수 있는 정보들이 나오는데, 대표적으로 클러스터의 크기, 중심, 제곱합 등이 있습니다.

결과 콘솔 창 상단에는 각 클러스터의 크기, 중심 좌표가 표시되어 있습니다.

결과 콘솔 창 중단에는 클러스터링 벡터가 있는데, 이는 각 데이터들의 소속 클러스터 정보를 담고 있습니다.

콘솔 창 하단에는 제곱합 정보가 나와 있습니다.
이제 주성분분석 결과인 pca_data와 군집분석 결과인 kmeans_result를 이용해서 cluster plot을 그려 보겠습니다.
# 군집분석 결과 시각화
fviz_cluster(kmeans_result, data = pca_data, geom = "point", stand = F, ellipse = T)
X축은 제1주성분, Y축은 제2주성분으로 설정한 결과,
1번 클러스터는 중간 가격, 2번 클러스터는 높은 가격, 3번 클러스터는 낮은 가격의 다이아몬드로 구성되어 있을 확률이 높다는 것을 알 수 있습니다.
마지막으로 box-plot을 이용해 각 클러스터 별 다이아몬드의 가격 분포를 보이겠습니다.
# 클러스터 레이블 추가
diamonds$cluster = as.factor(kmeans_result$cluster)
# 가격 분포 시각화
ggplot(diamonds, aes(x = cluster, y = price, fill = cluster)) +
geom_boxplot() +
theme_minimal() +
labs(title = "Price Distribution by Cluster", x = "Cluster", y = "Price")

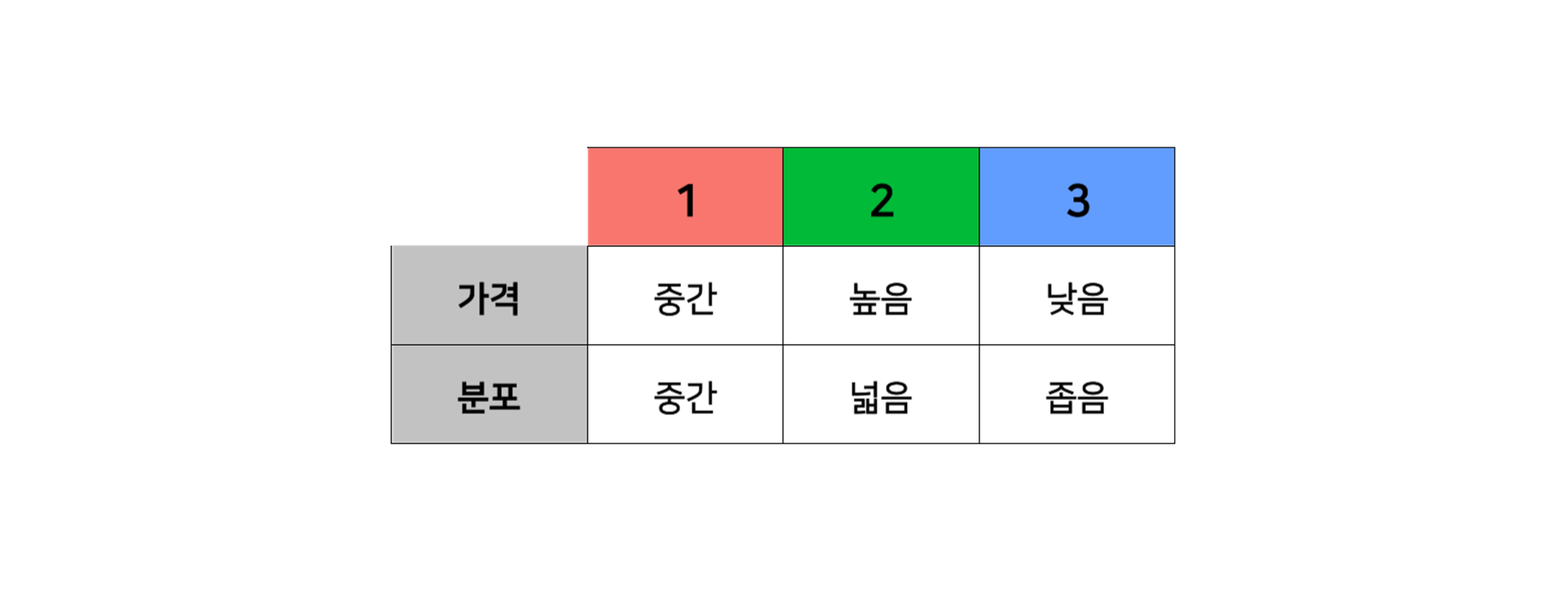
그 결과 위의 표와 같은 정보를 알 수 있었습니다.
결론
다이아몬드를 특정 속성들에 따라 주성분분석과 군집분석을 통해 세 가지 클러스터로 분류할 수 있었고, 각 클러스터 별로 다이아몬드의 가격이 유의미하게 차이가 난다는 것을 알 수 있었습니다.
3. 다이아몬드의 물리적 특성(carat, depth, table)과 시각적 특성(cut, color, clarity) 간에는 유의미한 상관 관계가 있다.
이 가설에서는 상관분석, 주성분분석, 정준상관분석을 사용하겠습니다.
먼저, 물리적 특성 간에 상관관계를 확인하기 위해 상관 행렬을 계산해보겠습니다.
## 상관분석
# 상관 행렬 계산
cor_matrix = cor(diamonds[, c("depth", "table", "x", "y", "z")])
cor_matrix
그 결과, x, y, z 간에는 매우 강한 양의 상관관계가 나타났습니다.
즉, 다이아몬드의 길이, 너비, 높이가 서로 밀접하게 관련되어 있음을 나타냅니다.
다음으로, 주성분분석을 통해 다이아몬드의 물리적 특성을 요약해보겠습니다.
## 주성분분석
# 주성분 분석 수행
diamonds_pca = prcomp(diamonds[, c("depth", "table", "x", "y", "z")], center = T, scale. = T)
diamonds_pca$rotation
summary(diamonds_pca)

주성분 분석의 결과, PC1, PC2가 각각 59.6%, 25.6%로 데이터의 변동성을 잘 설명하고 있으므로, 두 개의 주성분만으로 전체 데이터의 변동의 85.2%를 설명하고 있으므로, 차원을 성공적으로 축소했다고 할 수 있습니다.
다음으로, color와 clarity에 따라 데이터가 어떤 분포를 보이는지 시각화 해보겠습니다.

이 그래프는 시각적 특성인 color와 clarity에 따라 데이터가 어떻게 분포되는지를 보여줍니다.
clarity의 값이 높을수록 PC1 값이 높은데, 이는 PC1이 clarity 변동성을 많이 설명하고 있다는 것을 의미합니다.
color의 경우, 등급이 낮을 수록 PC1의 값이 높아지는 것으로 보입니다.
마지막으로, 정준상관분석(CCA)을 통해 물리적 특성 시각적 특성 간의 관계를 분석했습니다.
물리적 특성 변수로는 carat, depth, table, 시각적 특성 변수로는 cut, color, clarity를 선택했습니다.
## 정준상관분석
library(CCA)
# 물리적 특성 변수 선택
phys_vars = diamonds[, c('carat', 'depth', 'table')]
# 시각적 품질 변수 선택 (범주형 변수를 수치형으로 변환)
diamonds$cut = as.numeric(as.factor(diamonds$cut))
diamonds$color = as.numeric(as.factor(diamonds$color))
diamonds$clarity = as.numeric(as.factor(diamonds$clarity))
visual_vars = diamonds[, c('cut', 'color', 'clarity')]
# 정준상관분석 수행
cca_result = CCA::cc(phys_vars, visual_vars)
# 정준상관계수
cca_cor = cca_result$cor
print(cca_cor)
# 고유값 (정준상관계수의 제곱)
cca_eigenvalues = cca_cor^2
print(cca_eigenvalues)
이 결과는 물리적 특성과 시각적 특성 간에 유의미한 상관관계가 있음을 보여줍니다.
특히 첫번째 정준상관계수가 0.59로, 두 변수군 간에 상당한 관계가 있음을 나타냅니다.
두 번째 정준상관계수는 0.41로, 여전히 유의미한 상관관계를 보여줍니다.
그러나 세 번째 정준상관계수는 0.03으로, 거의 관계가 없음을 나타냅니다.
고유값을 살펴보면, 첫 번째 정준변수 쌍은 전체 변동성의 약 35.25%를 설명합니다.
이는 물리적 특성과 시각적 특성 간의 관계에서 상당히 큰 부분을 차지합니다.
두 번째 정준변수 쌍은 약 16.99%를 설명하며, 역시 의미 있는 설명력을 가지고 있습니다.
그러나 세 번째 정준변수 쌍은 변동성의 거의 0.07%만을 설명하여, 무시할 수 있는 수준입니다.
또한, 정준변수 계수를 통해 각 변수의 기여도를 확인해보았습니다.
# 정준변수 계수
xcoef = cca_result$xcoef
ycoef = cca_result$ycoef
print(xcoef)
print(ycoef)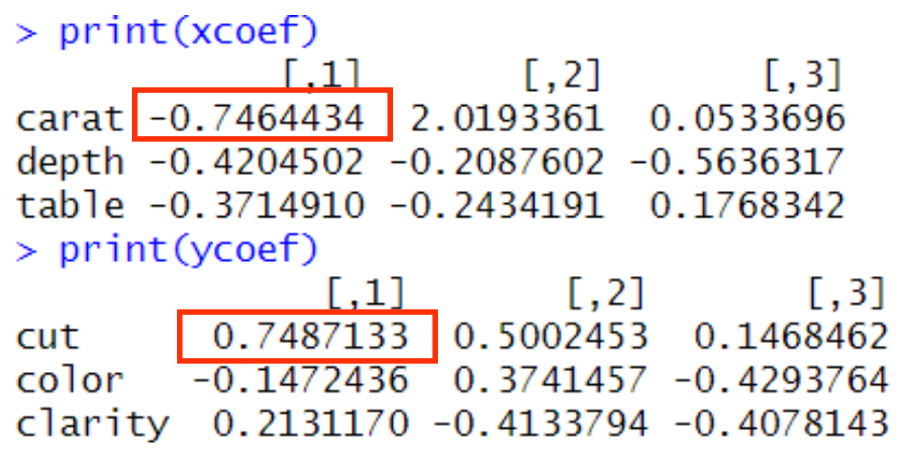
물리적 특성에서는 carat, 시각적 특성에서는 cut이 중요한 역할을 하고 있음을 알 수 있습니다.
결론
이 분석을 통해 다이아몬드의 물리적 특성과 시각적 특성 간의 관계를 이해할 수 있었습니다.
상관분석을 통해 변수 간의 기본적인 상관관계를 확인하고, 주성분분석을 통해 데이터의 주요 변동성을 요약했으며, 정준상관분석을 통해 두 변수군 간의 상관관계를 명확히 파악할 수 있었습니다.
지금까지 diamonds 데이터에 기반한 세 가지 가설을 세우고 검정해보았습니다.
감사합니다.
'R' 카테고리의 다른 글
| [R] 다변량 자료 분석 (2) : Hotelling T^2 검정 (2) | 2024.03.21 |
|---|---|
| [R] 다변량 자료 분석 (1) : airquality 데이터 산점도 (0) | 2024.03.21 |
| [R] 데이터 전처리 및 시각화 (4) (0) | 2024.02.23 |
| [R] 데이터 전처리 및 시각화 (3) (0) | 2024.01.23 |
| [R] 데이터 전처리 및 시각화 (2) (1) | 2024.01.23 |



